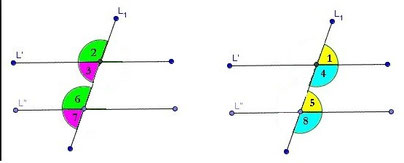
Ángulos con dos Rectas Paralelas y una Transversa.
ángulos Opuestos al Vértice: Son aquellos que están del lado contrario respecto al vértice.
Ángulos correspondientes: Son aquellos que están del mismo lado de la transversal y además miden lo mismo.
A + 78० = 180०
A = 180० - 78०
A = 102०
A=102० B=78० C=78० D=102०
E=102० F= 78० G=78० H=102०
C = 6x+3 H = 5x+10
6x+3+5x+10=180०
6x+5x=180-10-3
7x=180-13
x=167/11
x=15.18
6(15.18)+3=94.08
5(15.18)+10=85.9
A=85.9० B=94.08० C=94.08० D=85.9० E=85.9० F=94.08० G=94.08० H=85.9०
Nota: Cuando los dos ángulos son opuestos se realiza el mismo procedimiento pero en lugar de igualar la operación a 180, se igualan entre ellas (una igualdad): A=B.
Video Tutoorial: https://youtu.be/2OPoYzg_E58
Fuentes: Clase de Mate ;)